DAG のトポロジカルソート
書いたことはあったが、やり方を忘れていて悲しかったので、簡単にまとめておく。
DAG (Directed Acyclic Graph) とは、閉路を持たない有向グラフのことを指す、有向非巡回グラフである。
トポロジカルソートとは、この DAG の頂点をどのノードもその出力辺の先の頂点より前に来るように並べることである。
下の図を見た方が分かりやすいかもしれない。
例えば、以下のようなグラフがあったとする。
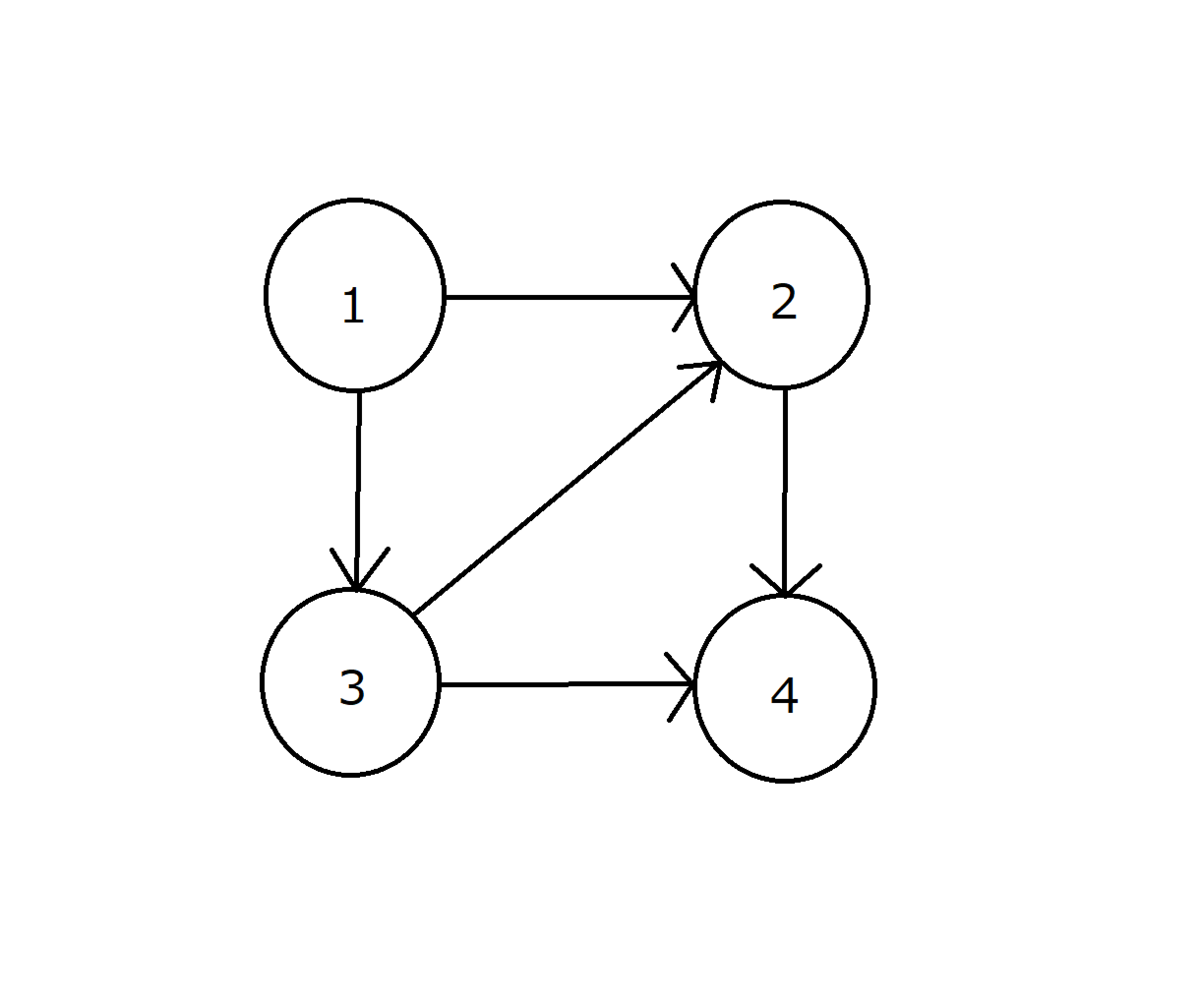
これをトポロジカルソートすると、下図のようになる。
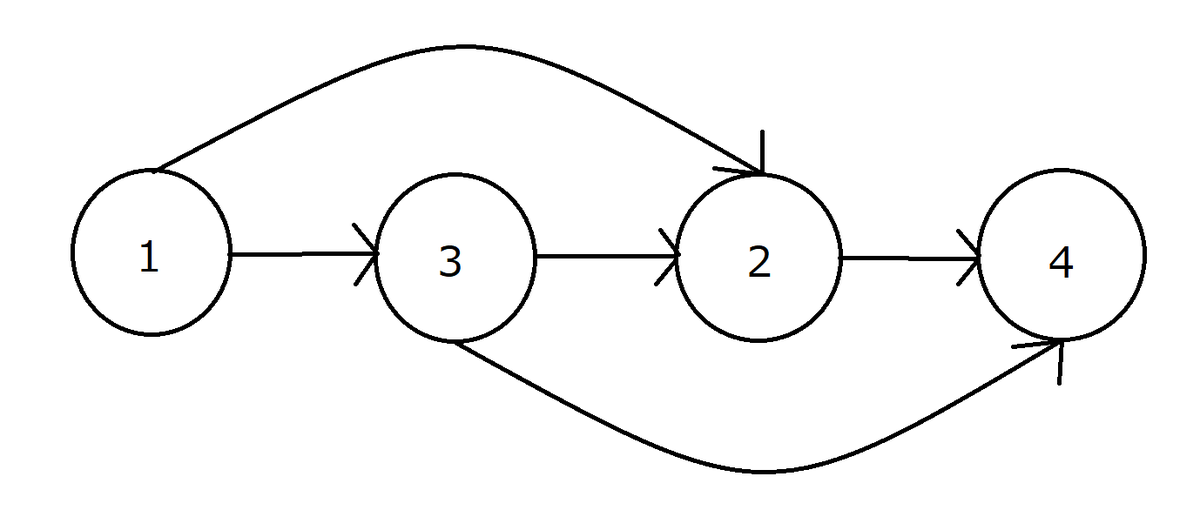
トポロジカルソートによって、有向辺が右向きのみとなっている。
トポロジカルソートは以下の操作で行える。
- ある頂点を始点として、深さ優先探索を行う。(頂点に訪問したときにフラグを立てておく。)
- これを全頂点について行い、辿った頂点を帰りがけ順でコンテナに保存しておく。(この逆順がトポロジカルソートされた頂点の並びとなる。)
全頂点に対して行うのは、トポロジカルソートにおいて途中の頂点から深さ優先探索を行っていたときや、グラフに非連結な部分あるときに対応するためである。
どちらとも単一始点からのみ行ってしまうと、網羅できない部分が存在してしまう。
また、今回の例では並べ方は一通りであったが、グラフによっては複数通りあるときもある。
ソースコードの一例を上げておく。
#include <iostream> #include <vector> #include <algorithm> using namespace std; int V; // 頂点数 vector<int> graph[100005]; // DAG vector<int> order; // トポロジカルソートされた頂点を格納 bool used[100005]; // 訪問済みフラグ // 辿れるところまで辿る深さ優先探索 void dfs(int u){ if(used[u]) return; used[u] = true; for(int v : graph[u]) dfs(v); order.push_back(u); // 帰りがけ順で頂点を入れていく } // トポロジカルソート void tsort(){ for(int v = 0; v < V; ++v) dfs(v); reverse(order.begin(), order.end()); }
入次数を管理することでソートする方法もあるが、ここでは割愛する (気が向いたら付け足すかもしれない) 。
【雑記】
FFT について書こうと思っていたが、理解しきれていないのでとりあえず断念。
年が明けても相変わらず何もしていない。
追記 (2020/5/9)
入次数を管理してトポロジカルソートをするコードを載せておく。
入次数が の頂点を見つけるたびにキューに入れていくと、キューに入った順がトポロジカル昇順となる。
キューから取り出した頂点をコンテナに入れておき、その頂点から到達できる頂点の入次数をデクリメントするという操作を繰り返していけばよい。
#include <iostream> #include <vector> #include <algorithm> #include <queue> using namespace std; // 注 : resize() などは適当に int V; // 頂点数 vector<int> graph[100005]; // DAG vector<int> order; // トポロジカルソートされた頂点を格納 vector<int> in; // 入次数 vector<int> idx; // トポロジカル順序で何番目か void tsort(){ queue<int> que; for(int v = 0; v < V; ++v){ if(in[v] == 0){ que.push(v); } } while(!que.empty()){ int u = que.front(); que.pop(); // トポロジカル順序の情報を格納 idx[u] = order.size(); // キューから取り出された頂点をコンテナに入れる order.push_back(u); for(int v : graph[u]){ // 入次数 = 0 であれば、キューに入れる if(--in[v] == 0){ que.push(v); } } } }
(2020/07/18)
DAG ⇔ トポロジカルソート可能
この同値関係を使って解く類題が Codeforces で出たが、辿り着くまでに時間がかかってしまったのでメモ。(詰め切れなくて解けなかった...)
有向グラフに閉路があるときは、トポロジカルソートをしてもコンテナに入っている頂点数が等しくならない。
AOJ の類題も載せておく。